ALU
The ALU is the chip responsible for doing all the math that happens in the CPU. The chips you have to implement are:
- HalfAdder - designed to add two bits
- FullAdder - designed to add three bits
- Add16 - designed to add two 16 bit numbers
- Inc16 - adds the constant 1 to a given numer
- ALU - the arithmetic logic unit, responsible for math operations
Vist this PDF for more hints and details: Download
I’ll cover the ALU specifically because its the most complex one of in this section.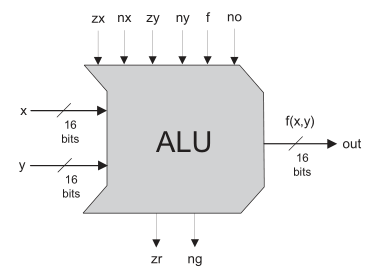
- Chip name: ALU
- Inputs:
- x[16], y[16], // Two 16-bit data inputs
- zx, // Zero the x input
- nx, // Negate the x input
- zy, // Zero the y input
- ny, // Negate the y input
- f, // Function code: 1 for Add, 0 for And
- no // Negate the out output
- Outputs:
- out[16], // 16-bit output
- zr, // True iff out=0
- ng // True iff out<0
- Function:
- if zx then x = 0 // 16-bit zero constant
- if nx then x = !x // Bit-wise negation
- if zy then y = 0 // 16-bit zero constant
- if ny then y = !y // Bit-wise negation
- if f then out = x + y // Integer 2’s complement addition
else out = x & y // Bit-wise And - if no then out = !out // Bit-wise negation
- if out=0 then zr = 1 else zr = 0 // 16-bit eq. comparison
- if out<0 then ng = 1 else ng = 0 // 16-bit neg. comparison
Function:
| zx | nx | zy | ny | f | no | out |
|---|---|---|---|---|---|---|
| if zx then x=0 | if nx then x=!x | if zy then y=0 | if ny then y=!y | if f then out=x+y else out=x&y | if no then out=!out | f(x,y)= |
| 1 | 1 | 1 | 0 | 1 | 0 | -1 |
| 0 | 0 | 1 | 1 | 0 | 0 | x |
| 1 | 1 | 0 | 0 | 0 | 0 | y |
| 0 | 0 | 1 | 1 | 0 | 1 | !x |
| 1 | 1 | 0 | 0 | 0 | 1 | !y |
| 0 | 0 | 1 | 1 | 1 | 1 | -x |
| 1 | 1 | 0 | 0 | 1 | 1 | -y |
| 0 | 1 | 1 | 1 | 1 | 1 | x+1 |
| 1 | 1 | 0 | 1 | 1 | 1 | y+1 |
| 0 | 0 | 1 | 1 | 1 | 0 | x-1 |
| 1 | 1 | 0 | 0 | 1 | 0 | y-1 |
| 0 | 0 | 0 | 0 | 1 | 0 | x+y |
| 0 | 1 | 0 | 0 | 1 | 1 | x-y |
| 0 | 0 | 0 | 1 | 1 | 1 | y-x |
| 0 | 0 | 0 | 0 | 0 | 0 | x&y |
| 0 | 1 | 0 | 1 | 0 | 1 | x|y |
There are 6 control bits being:
zx, nx, zy, ny, f, no
Each row corresponds to a series of transformation on the x and y input that constitute and build up to an overall function noted in the out column.
Let’s elaborate any row with any input, and let’s start with the row that adds 1 to the x input.
x + 1
increment x by 1 zx nx zy ny f no out 0 1 1 1 1 1 x+1 Following the table from left to right(~>) sequentially,
Say the inputs are:
x: 0111 (7)
y: 1011 (doesn’t really matter since we only want to increment x by 1 here.)
zx is 0, so we don’t do anything
nx is 1, so !x => 1000
zy is 1, so y = 0000
ny is 1 so y = 1111
f is 1, so we do 2’s complement addition on the transformed inputs:1000 + 1111 _________ 1[0111]
no is 1 so we negatate output:
!(0111) = 1000 (8)
and thus we have done x+1
y - x
subtracts the input Y by the input X zx nx zy ny f no out 0 0 0 1 1 1 y-x
Let’s say our inputs are:
x: 0100 (4)
y: 1001 (9)
We’re trying to do 9-4 = 5. Let’s see if we achieve this:
zx is 0, so we don’t do anything
nx is 0, so we don’t do anything
zy is 0, so we don’t do anything
ny is 1, so we negate !y = 0110
f is 1, so we do 2’s complement addition on the transformed inputs:0100 + 0110 _________ 1010
no is 1 so we negatate out above which will be 0101(5)!
9 - 4 = 5 , so we are good
Try it yourself! Elaborate any row with random inputs you can come up with.